Obrigado a Julio Marchi pelo espaço cedido na MSX All
  

Curso de Jogos



8-Puzzle


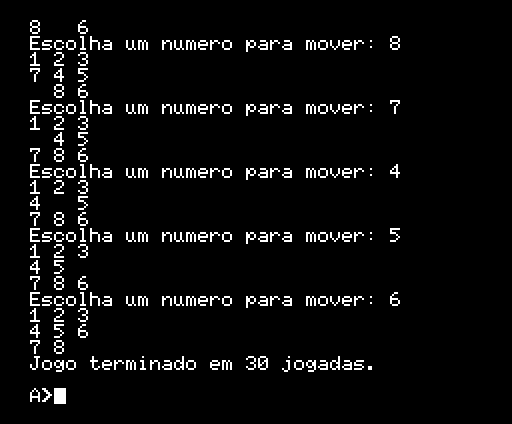
  English

  Jogo de quebra cabeças que consiste em ordenar 8 peças em um tabuleiro de 3x3 quadrados, movendo sempre os números para o buraco.
  Esse jogo é uma variação do N-Puzzle, onde possui diversas versões como o 8-Puzzle, 15-Puzzle, 24-Puzzle etc.


1. A Construção do Jogo
  O jogo será programado em C, que também serve para o PC. Entretanto, poderá ser facilmente portado para Pascal.


  Tabuleiro do jogo

  O tabuleiro do jogo poderá ser feito em uma matriz de 3x3 ou um vetor de 9 posições. Serão apresentadas ambas as soluções.

Matriz 3x3 Vetor de 9 
int board[3][3], HX, HY, moves;

int board[9], pos, moves;

  No caso da matriz de 3x3, devemos armazenar as coordenadas X e Y do buraco em HX e HY, respectivamente. Já no caso do vetor, armazenamos apenas a posição do buraco em pos. A variável moves armazena a quantidade de movimentos gastos pelo jogador para solucionar o jogo.
  Uma vez que os vetores e matrizes no C variam de 0 a N-1, as coordenadas ou posição do buraco irão também variar de 0 a N-1. Entretanto, os rótulos dos números variam de 1 a 8. Dessa forma, deve-se tomar cuidado quanto a essa questão.
  Os valores iniciais do jogo não poderão apresentar qualquer seqüência aleatória, pois poderia resultar em um jogo sem solução possível. Dessa forma, a solução para obter uma seqüência inicial válida será a mesma adotada no jogo real: a partir da seqüência ordenada, faremos N movimentos no sentido de embaralhar o jogo.


  Embaralhando

  Primeiramente, uma função irá colocar os números de 1 a 8 de forma ordenada, reservando para o buraco o valor 0.

Matriz 3x3 Vetor de 9 
void end_board()
{
  int x,y,val=1;

  for (y=0; y<3; y++)
  {
    for (x=0; x<3; x++)
      board[x][y] = val++;
  }

  board[2][2] = 0;
  HX=2;
  HY=2;
}

void end_board()
{
  int p,val=1;

  for (p=0; plt&;9; p++)
    board[p] = val++;

  board[8] = 0;
  pos=8;
}

  Em seguida, é necessário realizar N movimentos sucessivos para embaralhar os números. Entretanto, é necessário antes ver como analisamos as trocas possíveis para um determinado buraco.


  Movimentos possíveis

  A análise dos movimentos possíveis é feita sempre a partir da posição buraco.
  Para a matriz 3x3, a análise é feita em tempo de execução. A partir de um deslocamento proposto dx e dy da posição do buraco HX e HX, verificamos se:
  • As coordenadas resultantes HX+dx e HY+dy caem dentro dos limites do tabuleiro;
  • A soma de dx e dy NÃO é igual a 0 (buraco não move); e
  • A soma de dx e dy NÃO é maior que 1 (anda em diagonal).
  Obs: -1 < dx < 1 e -1 < dy < 1

  Para o vetor de 9, armazenaremos em um vetor de strings todos os movimentos possíveis para cada posição do buraco. A troca é feita diretamente entre a posição do buraco e a possível.
  A ilustração abaixo apresenta os movimentos possíveis (em verde) para cada posição do buraco (vermelho).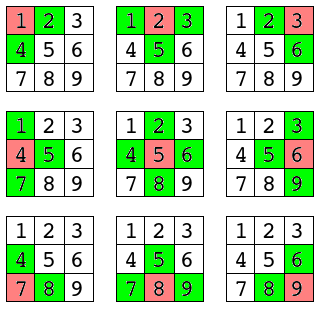

 

  Assim temos:

Vetor de 9 
char possible_moves[9][4] = {"24  ","135 ","26  ","157 ",
                             "2468","359 ","48  ","579 ",
                             "68  "};
int total_moves[9] = {2,3,2,3,4,3,2,3,2};

  Como o C não permite saber o tamanho da string, armazenamos a quantidade de movimentos no vetor total_moves.

  Os códigos para a troca de posições são:

Matriz 3x3 Vetor de 9 
int swap_pos(int x, int y)
{
  int temp;

  if ((x==HX) && (y==HY))
    return 0;

  if ((x>2) || (x<0) || (y>2) || (y<0))
    return 0; 

  if (abs(HX-x)+abs(HY-y) > 1)
    return 0;

  temp = board[HX][HY];
  board[HX][HY] = board[x][y];
  board[x][y] = temp;

  HX=x;
  HY=y;

  return 1;
}

int get_pm_value(int i)
{
  return (int) possible_moves[pos][i] - 49;
}

int valid_move(int p)
{
  int i, pp;

  for (i=0; i<4; i++)
  {
    pp = get_pm_value(i);
    if (pp == p)
      return 1;
  }

  return 0;
}

int swap_pos(int p)
{
  int temp;

  if ((p>8) || (p<0))
    return 0; 

  if (!valid_move(p))
    return 0;

  temp = board[pos];
  board[pos] = board[p];
  board[p] = temp;

  pos=p;

  return 1;
}

  No array de 9, o movimento possível é obtido através da conversão do código ASCII do caractere da posição para o valor numérico correspondente, na função get_pm_value. De forma a se adequar aos índices dos vetores e matrizes do C, a mesma função também converte o valor da posição para o sistema que varia de 0 até N-1. Exemplo desse processo em Basic: 
Q = "2"
P = ASC(Q) - 48
PRINT P
 2

P = P-1
PRINT P
 1
  Para ambos os casos, o parâmetro de entrada é a nova posição do buraco.
  Após realizar a troca, a posição nova do buraco é atualizada.


  Código para embaralhar

  Uma vez visto como se troca uma posição, podemos embaralhar.

Matriz 3x3 Vetor de 9 
void shuffle_board()
{
  int x,y,r,rounds=50;
  int flag;

  srand(time(NULL));

  for (r=1; r<=rounds; r++)
  {
    flag=0;
    while (flag!=1)
    {
      flag = 1;
      x=rand()%3 - 1;
      y=rand()%3 - 1;

      flag = swap_pos(HX+x,HY+y);
    }
  }
}

void shuffle_board()
{
  int i,p,r,rounds=50;

  srand(time(NULL));

  for (r=1; r<=rounds; r++)
  {
    i = rand()%total_moves[pos];
    p = get_pm_value(i);
    swap_pos(p);
  }
}

  No caso da matriz de 3x3 ele sorteia os valores dx e dy e somente segue adiante se o movimento for válido. Senão, tenta novos valores até conseguir.
  A solução do vetor de 9 é mais inteligente, pois permite escolher diretamente uma dos movimentos válidos para o buraco aramazenados no vetor possible_moves.


  Inicialização e impressão do jogo

  Os códigos a seguir completam a primeira etapa, onde uma função chama a inicialização do tabuleiro e outra o imprime.

Matriz 3x3 Vetor de 9 
void print_board()
{
  int x,y;

  for (y=0; y<3; y++)
  {
    for (x=0; x<3; x++)
    {
      if (board[x][y] == 0)
        printf("  ");
      else
        printf("%d ",board[x][y]);
    }
    printf("\n");
  }
}

void start_board()
{
  end_board();
  shuffle_board();
}

void print_board()
{
  int p;

  for (p=0; p<9; p++)
  {
    if (board[p] == 0)
      printf("  ");
    else
      printf("%d ",board[p]);

    if ((p+1) % 3 == 0)
      printf("\n");
  }
}

void start_board()
{
  end_board();
  shuffle_board();
}


2. Controlando o Jogador
  Esse jogo é para apenas um jogador. Assim, o programa deverá ler do teclado o número da peça que se deseja mover e realizar a troca. Para isso:
  • O número da peça deverá estar entre 1 e 8; e
  • O movimento deverá ser válido.
Matriz 3x3 e Vetor de 9 
void player_turn()
{
  int num, flag=0;

  while (flag!=1)
  {
    flag=1;
    printf("Escolha um numero para mover: ");
    scanf("%d",&num);

    if ((num < 1) || (num > 8))
    {
      flag=0;
      printf("O numero deve ser entre 1 e 8!\n");
    }

    if (move_square(num)!=1)
    {
      flag=0;
      printf("O numero %d nao pode ser movido!\n",num);
     }
  }
}


  Convertendo o número da peça em posição no tabuleiro

  O dado fornecido pelo jogador é o número da peça e não uma coordenada. Assim, o programa tem que localizá-la no tabuleiro.

Matriz 3x3 Vetor de 9 
void get_num_coords(int num, int *xx, int *yy)
{
  int x,y;

  for (y=0; y<3; y++)
  {
    for (x=0; x<3; x++)
    {
      if (board[x][y] == num)
      {
        *xx=x;
        *yy=y;
      }
    }
  }
}

void get_num_pos(int num, int *pp)
{
  int p;

  for (p=0; p<9; p++)
  {
    if (board[p] == num)
      *pp=p;
  }
}


  Realizando a troca

  Após localizar a peça requerida, é só fazer a troca.

Matriz 3x3 Vetor de 9 
int move_square(int num)
{
  int x,y;

  get_num_coords(num, &x, &y);

  if (swap_pos(x,y)!=1)
    return 0;

  return 1;
}

int move_square(int num)
{
  int p;

  get_num_pos(num, &p);

  if (swap_pos(p)!=1)
    return 0;

  return 1;
}

  Caso o movimento seja inválido, a função notifica retornando 0.


  Verificando o fim de jogo

  A rotina de verificação se o jogo foi solucionado é bem simples, pois basta constatar que os números estão em ordem no tabuleiro.

Matriz 3x3 Vetor de 9 
int check_win()
{
  int x,y,num=1;

  for (y=0; y<3; y++)
  {
    for (x=0; x<3; x++)
    {
      if (board[x][y] != (num++ % 9))
        return 0;
    }
  }

  return 1;
}

int check_win()
{
  int p,num=1;

  for (p=0; p<9; p++)
  {
    if (board[p] != (num++ % 9))
      return 0;
  }

  return 1;
}

  Obs: quando a variável num for 9, ele deverá retornar a 0 para comparação com o buraco.


  Controle do jogo

  A seguinte rotina controla o jogo para ambos os casos.

Matriz 3x3 e Vetor de 9 
void game()
{
  moves=0;
  start_board();
  print_board();

  while (check_win()!=1)
  {
    player_turn();
    moves++;
    print_board();
  }

  printf("Jogo terminado em %d jogadas.\n",moves);
}

main()
{
  game();
}


3. Download
  As versões completas do jogo, segundo cada solução proposta, podem ser obtidas aqui.

  8puzzle.zip - Jogo em C

  Programa em C: Marcelo Silveira

  Jogo adaptado de [1].


  Referências:

  [1]- Inteligência Artificial em Basic, M. James, Editora Campus, 1985.
Marcelo Silveira
Engenheiro de Sistemas e Computação
Especialista em Processamento de Imagens e Inteligência Artificial
© MarMSX 1999-2025