Inteligência Artificial
Redes Neurais - Backpropagation


Você está em: MarMSX >> Cursos >> AI   Vimos no capítulo anterior o que é uma rede neural e como o sinal se propaga pela rede, prevendo corretamente o que aprendeu. Entretanto, o programa criado naquele capítulo não tem a capacidade de fazer com que os neurônios sejam ajustados e aprendam coisas novas. Sem o aprendizado, a rede fica parada no tempo e no espaço.
  O objetivo desse capítulo é apresentar uma técnica de ajustamento de pesos chamada de gradient decent (descida do gradiente), que nos permitirá fazer com que a rede seja capaz de aprender.
Backpropagation - Gradient Descent   No perceptron, o ajustamento dos pesos é relativamente simples porque podemos calcular o erro de saída diretamente no perceptron, ou seja, sabemos qual valor de saída esperar dele e calcular o erro. De acordo com a Regra de Hebb [1]: 
ΔWij = η * Si * ej
  Onde:
  Graficamente:   O mesmo é válido para os pesos que se ligam à camada de saída em uma rede neural, pois, conhecemos os valores que estes neurônios devem apresentar no treinamento.
  Para calcular os pesos nas camadas escondidas, necessitamos conhecer os erros dos neurônios dessas camadas. Porém, como podemos calcular os erros dos neurônios localizados nas camadas escondidas, se não sabemos que valores eles devem apresentar?
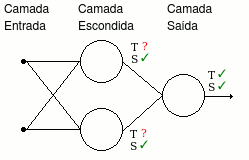  É ai que surgem os algoritmos de backpropagation (retro propagação).
  A idéia desses algoritmos é propagar os erros calculados nos neurônios de saída no sentido inverso da rede, ajustando os pesos a partir dos sinais retro-propagados. Devemos ressaltar que o sucesso que as redes neurais fazem hoje se devem à criação desses algoritmos.
  Veja na ilustração abaixo como o erro obtido na camada de saída é propagado no sentido inverso da rede.
  A partir do erro calculado em cada neurônio da camada de saída, multiplicamos esses valores pela derivada F '(x) da função de ativação F(x) dos neurônios dessa camada, onde x é o sinal Sj calculado durante a etapa de feed forward. A combinação do erro mais a derivada da função de ativação produz uma saída ej no neurônio, no sentido inverso da rede.
  Assim, temos para os neurônios da camada de saída: 
ej = (Tj-Sj) * F'(x)

  As funções de ativação F(x) e suas respectivas derivadas F '(x) são apresentadas a seguir.
  A função de ativação da última camada normalmente é uma função linear. Nesse caso, temos: 
ej = (Tj-Sj) * 1

  Uma vez calculado o valor de ej, podemos ajustar os pesos entre a camada escondida e a camada de saída, e também o bias da camada de saída. Em ambos os casos, utilizamos a regra de Hebb: 
Wij = Wij + η * Si * ej
Biasj = Biasj + η * ej
  Onde Si é a saída do neurônio da camada escondida, obtida na etapa de feed forward (sentido para frente).

  Observe a ilustração a seguir.
  O ajuste dos pesos e bias é feito desta maneira para qualquer camada da rede. Porém, o cálculo de ei, ou seja, o erro propagado pelos neurônios da camada escondida i é um pouco diferente. Isto porque, nessa camada, cada neurônio pode receber o sinal de diversos outros neurônios. Veja a ilustração a seguir.
  Observando a ilustração anterior, concluímos que: 
ei = (Σ ej * Wij) * F'(x)

  A função de ativação da camada escondida pode ser a sigmóide ou a tansig. Lembremos que o valor de x é o sinal Si do neurônio i da camada escondida obtido na etapa de feed forward.
  Assim temos, para a função de ativação Tansig: 
ei = (Σ ej * Wij) * {1 - [2 / (1 + e-2*Si)]2}

  Para cada camada, podemos utilizar o seguinte cálculo matricial:
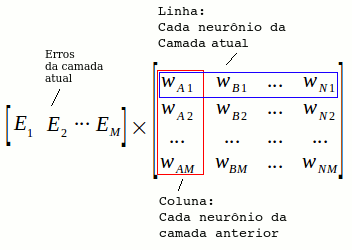  Na seção seguinte, veremos como construir o algoritmo de backpropagation.
O algoritmo de aprendizado por backpropagation gradient descent   A seguir, apresentamos o algoritmo completo de aprendizado por backpropagation gradient descent.
  1. Inicializar os pesos com valores aleatórios entre -1 e 1.
  2. Para cada amostra do conjunto de treinamento, fazemos o seguinte:
  3. Calculamos o MSE de todas as amostras de treinamento.
  4. Se número de épocas for menor que o máximo de épocas, vá para 2.

  A inicialização dos pesos pode ser feita com valores aleatórios entre -1 e 1. Entretanto, recomenda-se utilizar uma distribuição aleatória normal [5] para os pesos.

  O cálculo do MSE pode ser feito da seguinte maneira: 
e = Σ (Ti - Si)2 / (2 * N)
  Onde N é o número de neurônios da camada de saída.

  Em pseudo-algoritmo, temos: 
erro ← 0.0;

PARA i ← 1 até N FAÇA
  erro ← erro + (T[i] - S[i]) ^ 2;
FIM_PARA

erro ← erro / (2.0 * N);

  Para o MSE total, calculamos a soma dos MSEs das amostras e dividimos por duas vezes o números de amostras de teste.

  No arquivo programas da seção extra em C, na pasta RNA_BP, há dois exemplos em C do treinamento e teste de uma rede neural. Um aplica o treinamento ao caso do XOR, e outra à flor íris [2].
  Nesses arquivos, podemos chamar funções para exibir o status dos pesos e bias, bem como apresentar a arquitetura da rede.

  Veja o exemplo do treinamento e teste para o XOR: 
Epoca 100/2000, MSE: 0.13
Epoca 200/2000, MSE: 0.12
Epoca 300/2000, MSE: 0.09
Epoca 400/2000, MSE: 0.06
Epoca 500/2000, MSE: 0.03
Epoca 600/2000, MSE: 0.01
Epoca 700/2000, MSE: 0.00
Treinamento convergiu.

Teste:
Amostra 1
0.04621

Amostra 2
0.95583

Amostra 3
0.95010

Amostra 4
0.03624

  E para a flor íris: 
Epoca 100/2000, MSE: 0.05
Epoca 200/2000, MSE: 0.03
Epoca 300/2000, MSE: 0.02
Epoca 400/2000, MSE: 0.02
Epoca 500/2000, MSE: 0.02
Epoca 600/2000, MSE: 0.02
Epoca 700/2000, MSE: 0.02
Epoca 800/2000, MSE: 0.02
Epoca 900/2000, MSE: 0.02
Epoca 1000/2000, MSE: 0.02
Epoca 1100/2000, MSE: 0.02
Epoca 1200/2000, MSE: 0.02
Epoca 1300/2000, MSE: 0.02
Epoca 1400/2000, MSE: 0.02
Epoca 1500/2000, MSE: 0.02
Epoca 1600/2000, MSE: 0.02
Epoca 1700/2000, MSE: 0.02
Epoca 1800/2000, MSE: 0.02
Epoca 1900/2000, MSE: 0.02
Epoca 2000/2000, MSE: 0.02

Teste:
Numero de amostras: 45
Acertos: 43 (95.56 %)

  Há algoritmos de aprendizado mais eficientes, onde, por exemplo, o backpropagation é feito em lotes (batch). Isto signifca que somente há retro-propagação, quando todo o conjunto de treinamento é avaliado em feed-forward [1]. Para maiores informações, pesquise em [1] no capítulo de "Multilayer perceptrons".



  Referências

  1. Redes Neurais: Princípios e Prática, Simon Haykin. Ed. Bookman, 2001.
  2. Iris, Repositório de dados da UCI. Em http://archive.ics.uci.edu/ml/index.php
  3. GNU Octave. Em: https://www.gnu.org/software/octave/index
  4. Simple neural network implementation in c, Towards data science. Em: https://towardsdatascience.com/simple-neural-network-implementation-in-c-663f51447547
  5. Weight initialization techniques in neural networks, Towards data science. Em: https://towardsdatascience.com/weight-initialization-techniques-in-neural-networks-26c649eb3b78


<< Anterior   AI   Próxima >>