Curso de Basic
Formas Geométricas
Você está em: MarMSX >> Cursos >> BASIC
O MSX possui excelente potencial gráfico para desenho de formas geométricas. Os livros da editora Aleph apresentam figuras bem legais, no qual é possível estudá-las e aprender alguns conceitos.
A figura do livro do Expert [1]
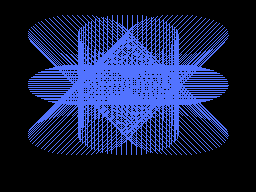
10 REM DRAWLIPSE 1
20 SCREEN 2
30 FOR A=0 TO 6.28 STEP .1
40 PSET(128+50*COS(A), 85+20*SIN(A)),5
50 DRAW"nu50nd50nr50nl50ne50nf50nng50nh50"
60 NEXT A
70 GOTO 70
Obtendo um ponto da superfície do círculo ou elipse
A obtenção de um ponto P(X,Y) da superfície de um círculo ou elipse é feito da seguinte maneira:
X = centro_X + raio_X * COS(ângulo)
Y = centro_Y + raio_Y * SIN(ângulo)
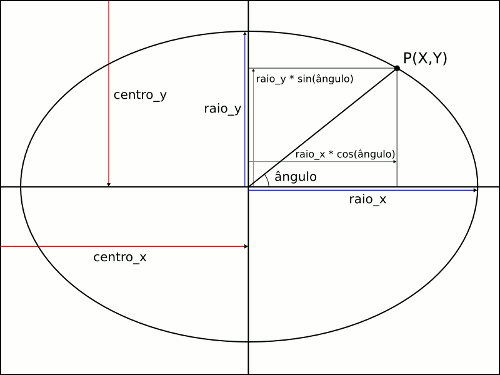
Esse conceito é importante para a compreensão de alguns desenhos geométricos feitos aqui.
Cesto [2]

10 SCREEN 2
20 PI=3.1415926#
30 CIRCLE(128,30),60,,,,20/60
40 CIRCLE(128,160),60,,,,20/60
50 D=PI/2
60 FOR AN=0 TO 2*PI STEP .15
70 X=128+60*COS(AN)
80 Y=30+20*SIN(AN)
90 S=128+60*COS(AN+D)
100 T=160+20*SIN(AN+D)
110 LINE(X,Y)-(S,T)
120 NEXT AN
130 GOTO 130
Esse desenho também se utiliza do ponto na superfície de uma elipse.
Ele traça uma linha de um ponto P1 localizado na elipse superior até um ponto P2 localizado na elipse inferior. Observe que há um deslocamento angular de 90 graus no ponto P2, para que a linha fique em diagonal.
Astróide 1 - Rede [2]

10 SCREEN 2
20 FOR F=0 TO 125 STEP 10
30 G=80-F*80/125
40 LINE(F,80)-(125,G)
50 LINE(125,G)-(250-F,80)
60 LINE(F,80)-(125,160-G)
70 LINE(125,160-G)-(250-F,80)
80 NEXT
90 GOTO 90
A figura base é um losango, que varia seus ângulos internos a cada iteração (loop).
Astróide 2 - Teia [2]

10 SCREEN 2
20 PI=3.1415926#
30 FOR A=10 TO 85 STEP 15
40 U=128+A
50 V=85
60 FOR T=0 TO 2*PI STEP.2
70 X=128+A*(COS(T)^3)
80 Y=85+A*(SIN(T)^3)
90 LINE(U,V)-(X,Y)
100 U=X : V=Y
110 IF A=85 THEN LINE(128,85)-(X,Y)
120 NEXT T,A
130 GOTO 130
A idéia é criar uma figura baseada nas funções seno(ângulo)3 e coseno(ângulo)3 em torno do ponto 128,85.
Esta figura é repetida, afastanto-se do centro de 15 em 15 pixels, controlado pela variável A.
Conforme dito no capítulo Plotando Gráficos, as funções normalmente geram pontos distantes entre si e estes devem ser ligados através de linhas (linha 90).
A linha 100 retém o último ponto plotado, para que na próxima iteração ele seja ligado ao novo ponto calculado.
A linha 110 traça uma linha do centro até o ponto atual, quando A=85 (última iteração).
Astróide 3 - Estrela [2]
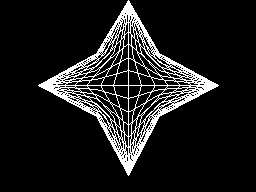
10 SCREEN 2
20 PI=3.1415926#
30 C=2*PI
40 I=PI/20
50 FOR F=1 TO 5
60 READ X(F),Y(F)
70 NEXT
80 DATA 0,100,35,35,100,0,35,-35,0,-100
90 FOR H=0 TO 1
100 FOR A=0 TO PI STEP I
110 FOR F=1 TO 5
120 X=X(F)*COS(A)
130 Y=Y(F)
140 S=X
150 X=-X*(H<>1)-Y*(H=1)
160 Y=-Y*(H<>1)-S*(H=1)
170 X=INT(X)
180 Y=INT(Y)
190 U=X*.9+128
200 V=Y*.9+85
210 IF F<>1 THEN LINE(K,L)-(U,V)
220 K=U:L=V
230 NEXT F,A,H
240 GOTO 240
Teste lógico
Há um teste lógico feito nas linhas 150 e 160, que tem como objetivo validar o não o uso das variáveis X e Y no cálculo.
Sintaxe:
T = -variável x teste_lógico
Possíveis valores obtidos:
T = variável ' Teste retornou -1 (verdadeiro)
T = 0 ' Teste retornou 0 (falso)
No caso da linha 150, X assume o valor igual a X, quando H é diferente de 1, e o valor igual a Y, quando H é igual a 1.
O sinal é invertido, porque o teste lógico em expressões no Basic retorna -1 quando verdadeiro.
Drawlipse [2]

10 SCREEN 2
20 FOR A=0 TO 6.28 STEP .1
30 PSET(128+50*COS(A), 85+20*SIN(A))
40 DRAW"nu50nf50nd50ng50"
50 NEXT A
60 FOR I=1 TO 5
70 READ X,Y
80 CIRCLE(X,Y),50,,,,.4
90 NEXT I
100 GOTO 100
110 DATA 128,34,128,135,128,85,77,135,178,135
Faz o desenho abaixo em torno de uma elipse. Ao final, reforça as elipses da figura.
|
/|\
Esfera [2]

10 SCREEN 2
20 FOR B=80 TO 1 STEP -10
30 CIRCLE(128,80),80,,,,80/B
40 CIRCLE(128,80),80,,,,B/80
50 NEXT B
60 LINE(128,160)-(128,0)
70 LINE(48,80)-(208,80)
80 GOTO 80
Nesse desenho são desenhadas elipses sobrepostas, variando-se o achatamento.
Osciloscópio [2]

10 PI=3.1415926#
20 IF STRIG(0)<>-1 AND P<>0 THEN 20
30 P=P+1
40 SCREEN 2
50 CIRCLE(128,85),84
60 FOR X=55 TO 200
70 Z=0
80 C=-X*(X=55)-C*(X<>55)
90 FOR M=1 TO P STEP 2
100 Y=80/(M*PI)*SIN(X*M*PI/36)
110 Z=Z+Y
120 NEXT
130 Y=Z+85
140 L=-Y*(X=55)-L*(X<>55)
150 LINE(C,L)-(X,Y)
160 PSET(X,Y)
170 C=X:L=Y
180 NEXT
190 P=P+1
200 GOTO 20
Anêmona [2]
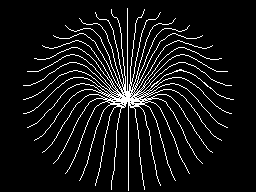
10 SCREEN 2
20 PI=3.1415926#
30 Q=2*PI : R=PI/20 : S=PI/10
40 T=60 : U=150/Q
50 FOR B=0 TO Q STEP R
60 C=T*PI/180
70 C=(B>PI)*C-(B<=PI)*C
80 FOR H=0 TO Q STEP S
90 Y=COS(H)*42
100 X=COS(B)*H*U
110 Z=-(SIN(B)=1)*H*U-(SIN(B)<>1)*TAN(B)*X
120 Z=ABS(Z)
130 Z=-1E-03*(Z=0)-Z*(Z<>0)
140 J=SQR(Z*Z+Y*Y)
150 A=ATN(Y/Z)+C
160 Y=J*SIN(A)
170 X=INT(X) : Y=INT(Y)
180 XP=X*.7+128
190 YP=Y*.7+85
200 XO=-XO*(H<>0)-XP*(H=0)
210 YO=-YO*(H<>0)-XP*(H=0)
220 LINE(XO,YO)-(XP,YP)
230 XO=XP
240 YO=YP
250 NEXT H,B
260 GOTO 260
Pétalas [2]

10 INPUT"Quantas petalas";P
20 INPUT"Com rotacao (s/n)";A$
30 PI=3.141592#
40 Q=2*PI
50 SCREEN 2
60 N1=5 : N2=4
70 FOR V=1 TO 10
80 I=V*PI/30*(A$="s")
90 M1=N1*V : M2=N2*V
100 FOR F=0 TO Q STEP Q/180
110 A=F-I
120 S=ABS(SIN(F*P/2))
130 R=S*M1+M2
140 X=COS(A)*R
150 Y=SIN(A)*R
160 GOSUB 220
170 X=INT(X) : Y=INT(Y)
180 NEXT F
190 GOSUB 220
200 NEXT V
210 GOTO 210
220 XP=X*.9+128
230 YP=191-(Y*.9+85)
240 IF F<>0 THEN 280
250 X1=X : Y1=Y
260 XO=XP : YO=YP
270 RETURN
280 LINE(XO,YO)-(XP,YP)
290 XO=XP : YO=YP
300 RETURN
Pétalas Coloridas

10 INPUT"Quantas petalas";P
20 INPUT"Com rotacao (s/n)";A$
30 PI=3.141592#
40 Q=2*PI : C=2
50 SCREEN 5
60 N1=5 : N2=4
70 FOR V=1 TO 7
75 PAINT(0,0),C
76 IF V<7 THEN C=C+1 ELSE C=1
77 COLOR C
80 I=V*PI/30*(A$="s")
90 M1=N1*V : M2=N2*V
100 FOR F=0 TO Q STEP Q/180
110 A=F-I
120 S=ABS(SIN(F*P/2))
130 R=S*M1+M2
140 X=COS(A)*R
150 Y=SIN(A)*R
160 GOSUB 220
170 X=INT(X) : Y=INT(Y)
180 NEXT F
190 GOSUB 220
200 NEXT V
205 PAINT(0,0),C
210 GOTO 210
220 XP=X*.9+128
230 YP=191-(Y*.9+85)
240 IF F<>0 THEN 280
250 X1=X : Y1=Y
260 XO=XP : YO=YP
270 RETURN
280 LINE(XO,YO)-(XP,YP)
290 XO=XP : YO=YP
300 RETURN
Referências
[1] - Livro: Dominando o Expert, editora Aleph, 5a. Edição, 1987.
[2] - Livro: Coleção de Programas para o MSX, Volume 1, editora Aleph, 1986.
[3] - Livro: Coleção de Programas para o MSX, Volume 2, editora Aleph, 1986.











