Curso de Assembly
Lógica Digital
Você está em: MarMSX >> Cursos >> Assembly Z80
É necessário entender um pouco de lógica digital para programarmos em Assembly. O objetivo é compreendermos os sistemas de numeração, de forma a diferenciar um número binário, decimal ou hexadecimal, além de conhecermos operações lógicas como E, OU, NÃO e OU Exclusivo.
1- Sistemas de Numeração
Sistema decimal
O sistema de numeração que usamos diariamente em nosso cotidiano é o sistema decimal. Ele é formado por dez algarismos distintos a saber: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. É a partir desses algarismos que formamos todos os outros números.
Um número decimal é composto por casas decimais, começando pela casa das unidades, passando pela dezenas, centenas, milhares e por aí vai. Por exemplo, o número 125 irá possuir:
Centena Dezena Unidade
1 2 5
O valor "1" está na casa das centenas, "2" está na casa das dezenas e "5" está na casa das unidades.
Quando aumentamos em uma unidade um número, se uma casa decimal possuir o algarismo máximo (9), o valor da casa decimal imediatamente à esquerda é incrementado (aumentado em uma unidade), e o valor da casa em questão é retornado ao algarismo mínimo (0). Quando há estouro do valor máximo de uma casa decimal, dizemos que "vai um".
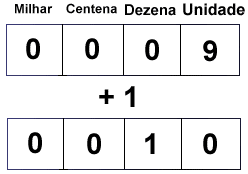
Para a soma de um número com um valor qualquer, o resultado da soma para aquela casa decimal quando "estoura" é o valor da casa da unidade da soma, e o "1" que sobra vai para a próxima casa decimal. Exemplo:
1
1 8
+ 4 8 + 4 = 12
-----
2 2
De forma análoga, quando diminuímos em uma unidade um determinada casa decimal contendo o valor mínimo (0), diminuímos em uma unidade a casa decimal imediatamente à sua esquerda, e a casa atual vai para o valor máximo (9). A essa operação dizemos que "pegamos emprestado" da próxima casa.
Passo 0 Passo 1 Passo 2
0
1 0 1 10 0 10
- 1 - 1 - 1
--- ----- -----
9 0 9
10-9=1 0-0=0
Sempre quando somamos ou subtraímos um número, fazemos a operação com as casas decimais equivalentes e aplicando as regras mencionadas, começando pela casa das unidades e partindo para as casas maiores. Exemplo:
<----
D U
2 5
+ 1 4
-----
3 9
Primeiros somamos 5 com 4, e depois 2 com 1.
A propriedade do "vai um" é transmissível às casas seguintes, quando há sucessivos "estouros". Exemplos:
Soma:
<-----
1 1
1 9 9
+ 1 5
-------
2 1 4
Subtração:
<-----
1 1
2 1 4 Unidades: 4-6 = pede emprestado = 14-6 = 8
- 2 6 Dezenas: 0-2 = pagou, mas também pede emprestado = 10-2 = 8
------- Centenas: 1-0 = pagou e quitou empréstimo = 1-0 = 1
1 8 8
Esses conceitos que aprendemos no Ensino Fundamental são importantes para a compreensão do flag "Carry" do Z80, que indica que houve estouro em uma operação aritmética.
Além do sistema decimal, existem ainda mais três sistemas de numeração utilizados em computação: binário, octal e hexadecimal.
Sistema binário
O sistema binário (no MSX é representado pelo prefixo &B) possui apenas 2 algarismos distintos: 0 e 1. A ordem crescente dos números é:
0, 1, ?
Não temos o algarismo 2 para representar o próximo número. E agora?
Simples! Seguindo a regra de formação dos números decimais, quando "estoura" uma casa, incrementamos a casa seguinte e retornamos a casa atual para zero. Assim, o próximo número binário seria "10". Logo, a seqüência fica:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, ...
Veja as operações a seguir utilizando números binários.
0 + 1:
0
+ 1
---
1
1 + 1:
1
1
+ 1 <---- Aqui houve estouro, pois "1" é o máximo valor de um número binário
---
10
10 + 1:
10
+ 1
---
11
11 + 1:
1
11
+ 1 <---- Aqui houve estouro, pois "1" é o máximo valor de um número binário
---
100
Observe que essa regra se aplica para incrementos e decrementos. Para soma ou subtração entre números, siga a mesma regra utilizada pelo sistema decimal para somas ou subtrações desse tipo.
Exemplo de adição:
Decimal: Binário
1 111
15 011
+ 17 + 101
---- -----
32 1000
Ordem das somas: Ordem das somas:
1o.: 5 + 7 = 12 -> Vai um 1o.: 1 + 1 = 10 -> Vai um
2o.: 1 + 1 (+ 1) = 3 2o.: 1 + 0 (+ 1) = 10 -> Vai um
3o.: 0 + 1 (+ 1) = 10 -> Vai um
4o.: 0 + 0 (+ 1) = 1
Exemplo de subtração:
<--- sentido das subtrações
1
101
- 010
-----
011
Ordem das subtrações:
1o.: 1 - 0 = 1
2o.: 0 - 1 = pede emprestado = 10 - 1 = 1
3o.: 1 - 0 = paga = 0 - 0 = 1
A equivalência entre valores do sistema decimal e binário pode ser vista a seguir:
Decimal Binário
0 0
1 1
2 10
3 11
4 100
5 101
6 110
7 111
... ...
A conversão entre os sistemas binário e decimal podem ser feitas usando calculadoras ou o próprio Basic do MSX. Veja como:
' Binario para decimal
PRINT &B100 ↵
4
Ok
' Decimal para binario
PRINT BIN$(4) ↵
100
Ok
Observa-se que as operações lógicas do processador Z80 sobre números é feita sempre baseada em números binários.
Sistema octal
O sistema octal (no MSX é representado pelo prefixo &O) possui 8 algarismos distintos: 0, 1, 2, 3, 4, 5, 6 e 7.
A seqüência crescente desse sistema seria: 0, 1, 2, 3, 4,5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, ...
A conversão entre os sistemas octal e decimal podem ser feitas usando calculadoras ou o próprio Basic do MSX. Veja como:
' Octal para decimal
PRINT &O12 ↵
10
Ok
' Decimal para octal
PRINT OCT$(10) ↵
12
Ok
Esse sistema não é utilizado na programação Assembly.
Sistema hexadecimal
O sistema hexadecimal (no MSX é representado pelo prefixo &H) possui 16 algarismos. Devido ao fato dos caracteres numéricos serem baseados no sistema decimal, ficam faltando 6 algarismos, que serão representados pelas 6 primeiras letras do alfabeto. Assim, temos os seguintes algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
A seqüencia crescente em hexadecimal fica: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, ...
Quem já digitou programas em Assembly de revistas sobre MSX, percebeu-se de códigos como CD, C9, AB, etc. Agora você já sabe o que eles significam. São códigos de máquina representados no sistema de numeração hexadecimal.
A conversão entre os sistemas hexadecimal e decimal podem ser feitas usando calculadoras ou o próprio Basic do MSX. Veja como:
' Hexadecimal para decimal
PRINT &HF ↵
15
Ok
' Decimal para hexadecimal
PRINT HEX$(15) ↵
F
Ok
Em suma, temos:
- Hexadecimal - representam o código de máquina.
- Binário - base das operações do processador.
Vejamos uma tabela de equivalência numérica entre os sistemas:
|
Decimal |
Binário |
Octal |
Hexadecimal |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
| 2 |
10 |
2 |
2 |
| 3 |
11 |
3 |
3 |
| 4 |
100 |
4 |
4 |
| 5 |
101 |
5 |
5 |
| 6 |
110 |
6 |
6 |
| 7 |
111 |
7 |
7 |
| 8 |
1000 |
10 |
8 |
| 9 |
1001 |
11 |
9 |
| 10 |
1010 |
12 |
A |
| 11 |
1011 |
13 |
B |
| 12 |
1100 |
14 |
C |
| 13 |
1101 |
15 |
D |
| 14 |
1110 |
16 |
E |
| 15 |
1111 |
17 |
F |
| 16 |
10000 |
20 |
10 |
| 17 |
10001 |
21 |
11 |
| 18 |
10010 |
22 |
12 |
| 19 |
10011 |
23 |
13 |
O computador somente entende valores binários. Nós humanos, compreendemos melhor o sistema decimal. Dessa forma, os sistemas de numeração apenas mudam a representação de um mesmo valor, tornando-o mais compreensível tanto para um, como para o outro. Por exemplo, enquanto o computador entende o valor binário 1101, nós o convertemos para o seu correspondente em decimal e obtemos o valor 13, que é mais compreensível para nós. Entretanto, o valor é o mesmo em ambos os sistemas de numeração.
A nível de programação Assembly, não é necessário saber como converter entre os sistemas de numeração. Apenas, entender o que eles significam e como funcionam.
2- Operações lógicas
As operações lógicas tem como por objetivo testar uma ou mais entradas e produzir uma única saída. As operações lógicas mais usuais utilizam-se de duas entradas apenas.
Os principais operadores lógicos são os seguintes:
- AND - Faz operação lógica E, onde a saída é sempre verdadeira quando todas as entradas são verdadeiras.
- OR - Faz operação lógica OU, onde a saída é sempre verdadeira quando pelo menos uma das entradas é verdadeira.
- NOT - Faz operação lógica NÃO, onde a saída é a inversão da atribuição de verdadeiro ou falso da entrada.
- XOR - Faz operação lógica OU EXCLUSIVO, onde a saída é sempre verdadeira quando duas entradas são diferentes.
O operador AND
O operador AND (E, em português) tem como objetivo emitir uma saída verdadeira (valor 1), se e somente se todas as entradas forem verdadeiras.
Ex: Um jogo de futebol só pode ter início, quando o juiz e os dois assistentes estiverem presentes. Assim, temos:
SE (juiz_presente E assistente_1_presente E assistente_2_presente) ENTÃO jogo_começa
Se o valor de pelo menos um deles for falso (valor 0), o jogo não pode começar.
O operador OR
O operador OR (OU, em português) tem como objetivo emitir uma saída verdadeira (valor 1), se pelo menos uma das entradas for verdadeira.
Ex: Uma escola possui 3 técnicos em informática. Se pelo menos um deles estiver presente, o computador poderá ser consertado:
SE (tecnico_1_presente OU tecnico_2_presente OU tecnico_3_presente) ENTÃO conserta_computador
Basta a presença de um dos três técnicos para consertar o computador.
O operador NOT
O operador NOT (NÃO, em português) tem como objetivo inverter o valor de uma entrada. Se era falsa, torna-se verdadeira. Se era verdadeira, torna-se falsa.
Exs:
Belo → NÃO belo
Alto → NÃO alto.
O operador XOR
O operador XOR (OU Exclusivo, em português) tem como objetivo emitir uma saída verdadeira (valor 1), quando duas entradas são diferentes.
Ex: Diálogo da mãe com o filho: "escolhe, ou o carrinho ou a bicicleta. Escolhe só um!"
No caso, não é permitido deixar de escolher algo, bem como escolher as duas coisas.
Tabelas-verdade para os operadores
Uma tabela verdade é valoração das saídas para todas as combinações possíveis de entrada. Assim, temos:
| NOT |
| Entrada |
Saída |
| A |
S |
| 0 |
1 |
| 1 |
0 |
|
| AND |
| Entradas |
Saída |
| A |
B |
S |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
|
| OR |
| Entradas |
Saída |
| A |
B |
S |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
|
| XOR |
| Entradas |
Saída |
| A |
B |
S |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
Obs: O valor 0 corresponde ao falso, enquanto que o valor 1 corresponde ao verdadeiro.
Quando a operação lógica possui mais de duas entradas, aplica-se a operação em cascata. Por exemplo:
A AND B AND C = S
Faz-se primeiro o par A and B, obtendo-se a saída parcial S1. Depois, combina-se essa saída com a próxima entrada C, fazendo-se S1 and C, finalmente obtendo-se S.
Passo 0: A AND B AND C = S
Passo 1: A AND B = S1
Passo 2: S1 AND C = S
Como testar as operações lógicas em Basic:
PRINT 0 AND 1 ↵
0
PRINT 1 OR 0 ↵
1
PRINT 1 XOR 0 ↵
1
No arquivo do curso, há dois programas em Basic para brincar com as portas lógicas: PORTAE.BAS e PORTAOU.BAS.
2.1- Operações lógicas com números
As operações lógicas envolvendo números em qualquer sistema de numeração será feita bit a bit, ou seja, no sistema binário. Assim, devemos:
- Converter os números de um sistema qualquer para o sistema binário.
- Realizar a operação lógica.
- Converter o resultado final para o sistema original.
Exemplo:
14 AND 4
Passo 1: converter os números para binário.
14 = &B1110
4 = &B100
Passo 2: realizar a operação lógica, bit a bit, ou seja, casa decimal a casa decimal, assim como nas operações de soma e subtração.
1 1 1 0
E 0 1 0 0 0 E 0 = 0
----------
0
1 1 1 0
E 0 1 0 0 1 E 0 = 0
----------
0 0
1 1 1 0
E 0 1 0 0 1 E 1 = 1
----------
1 0 0
1 1 1 0
E 0 1 0 0 1 E 0 = 0
----------
0 1 0 0
Passo 3: converter de volta para o sistema original.
&B0100 = 4
Conferindo no Basic:
PRINT 14 AND 4 ↵
4
Ok
3- Testes lógicos
No Basic, os operadores de teste lógicos são os seguintes:
- = - igual
- <> - diferente
- > - maior
- < - menor
- >= - maior ou igual
- <= - menor ou igual
Um teste lógico envolve um ou mais operandos, que resultam em uma única saída, valorada em verdadeiro ou falso. Exemplos:
5 > 6 -> falso
4 <= 5 -> verdadeiro
3 = 3 -> verdadeiro
Realizamos um teste em Basic através da cláusula IF, que pode tomar dois caminhos dependendo da valoração verdadeira ou falsa. Exemplo:
IF 5>6 THEN PRINT"Verdadeiro" ELSE PRINT"Falso" ↵
Falso
Em Assembly, não há a clausula IF e tampouco os operadores apresentados. O teste lógico é feito através de uma comparação entre o registrador A e outro registrador de 8 bits, através da instrução CP. Essa operação faz a subtração de A pelo registrador sem acumular o resultado, mas setando os flags.
Assim, teremos as seguintes situações para CP:
- O resultado da conta é positivo, se A >= registrador.
- O resultado da conta é zero, se A = registrador.
- O resultado da conta é negativo, se A < registrador.
Exemplo:
LD A,5 ; A=5
LD B,6 ; B=6
CP B ; Compara A com B, fazendo A-B
Nesse caso, o resultado da conta é negativo e constata-se que A é menor que B.
3.1 - Equivalências lógicas
Equivalências envolvendo maior igual e menor e igual:
Entrada Saída
A >= B 1 ELSE 0
fica:
A < B 0 ELSE 1
Entrada Saída
A <= B 1 ELSE 0
fica:
A > B 0 ELSE 1
Exemplo:
IF IDADE >= 18 THEN PRINT"Pode dirigir" ELSE PRINT"Não pode dirigir"
Equivale a:
IF IDADE < 18 THEN PRINT"Não pode dirigir" ELSE PRINT"Pode dirigir"
Quando realizamos a negação da entrada, negamos a saída também, que resulta na inversão das situações.
Equivalências envolvendo os operadores E e OU:
a) NOT (A AND B) = NOT(A) OR NOT(B)
b) NOT (A OR B) = NOT(A) AND NOT(B)
Exemplo:
IF IDADE >= 20 AND IDADE <= 30 THEN PRINT"Apto" ELSE PRINT"Não apto"
Equivale a:
IF IDADE < 20 OR IDADE > 30 THEN PRINT"Não apto" ELSE PRINT"Apto"
Graficamente:
0 20 30
+---------+---------+-----------+
Não apto | Apto | Não apto
4 - Álgebra com números de 8 bits
Antes de começarmos, vejamos alguns conceitos envolvendo números binários, a respeito do comprimento deles.
Conceitos:
- 4 dígitos = nibble (Ex: &B1010 = &HC)
- 8 dígitos = byte (Ex: &B10010000 = &H9A)
- 16 dígitos = word (Ex: &B1001000000011111 = &H100A)
Os números são lidos da direita para a esquerda. Sendo assim, para um número de 4 bits, tem-se:
bit 3 | bit 2 | bit 1 | bit 0
------+-------+-------+------
1 | 0 | 1 | 0
O bit 3 é a casa de maior valor, enquanto o bit 0 é a casa de menor valor.
Para um número de 8 bits, tem-se:
bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
------+-------+-------+-------+-------+-------+-------+-------+
1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
O bit mais significativo ou MSB é a casa mais alta do número binário. Para um número de 4 bits, é o bit 3. Para um número de 8 bits, é o bit 7.
O bit menos significativo ou LSB é a casa mais baixa e sempre será o bit 0.
Operações aritméticas
O processador Z80 sempre realiza operações aritméticas em cima de números de 8 ou 16 bits. Elas são de 8 bits, se o registrador envolvido for um registrador de 8 bits, como por exemplo, os registradores A, B, C, D, E. Elas são de 16 bits, se envolverem registradores de 16 bits como BC, DE, HL etc.
Um registrador de 8 bits será sempre representado por 8 bits, independente do valor dele. O valor dele varia de 0 a 255.
Exemplos:
Valor em decimal: 1
Valor 8 bits em binário: 00000001
Valor em decimal: 254
Valor 8 bits em binário: 11111110
Conforme já visto, as operações aritméticas começam pela casa mais à direita e caminham para as casas mais à esquerda.
Em Assembly, o registrador F possui dois flags (sinais, semáforos) que sinalizam um "estouro": um chamado de Half-Carry, que sinaliza um estouro localizado no bit 3 (nibble), e outro chamado de Carry, que sinaliza estouro localizado no bit 7 (byte).
Exemplo de estouro do "nibble":
1
bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
------+-------+-------+-------+-------+-------+-------+-------+
0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
+ 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
------------------------------------------------------------------
0 0 0 1 0 0 0 0
No exemplo acima, o bit 3 foi estourado. Assim, o flag de Half-Carry (denominado pela letra H) seria setado (valor igual a 1).
Exemplo de estouro do "byte":
1
bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
------+-------+-------+-------+-------+-------+-------+-------+
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
+ 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
------------------------------------------------------------------
0 0 0 0 0 0 0 0
Agora o bit 7 (além do 3) também foi "estourado". Assim, o flag de Carry (C) é setado. Observe que nesse caso, o número binário voltou a zero, pois o tamanho máximo do número binário é de 8 bits.
Na subtração, os flags H e C são setados quando há empréstimos e a última casa não consegue "pagar" tudo.
Exemplo de estouro do "nibble" para subtração:
1
bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
------+-------+-------+-------+-------+-------+-------+-------+
0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
- 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
------------------------------------------------------------------
0 0 0 0 1 1 1 1
O bit 3 não conseguiu "zerar" o empréstimo.
Exemplo de estouro do "byte" para subtração:
1
bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
------+-------+-------+-------+-------+-------+-------+-------+
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
- 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
------------------------------------------------------------------
1 1 1 1 1 1 1 1
O bit 7 não conseguiu "zerar" o empréstimo (além do bit 3 - H e C setados).
5- Números binários positivos e negativos
5.1- Complemento
O complemento de um número é a inversão de todos os bits desse número. Corresponde ao operador lógico bit a bit NOT aplicado a um número. Exemplo:
NOT
1100 ----> 0011
Devemos lembrar que o MSX representa seus números em 8 ou 16 bits. Assim, a operação anterior ficaria em 8 bits:
NOT
00001100 ----> 11110011
E em 16 bits:
NOT
0000000000001100 ----> 1111111111110011
5.2- Números não sinalizados
Os números inteiros não sinalizados utilizam toda a faixa de valores correspondente ao tamanho do número (8, 16, 32 etc bits) para representar números inteiros positivos. Assim, temos:
8 bits - 0 a 255
16 bits - 0 a 65535
32 bits - 0 a 4294967295
...
Os valores variam de 0 a 2n-1, onde n é o número de bits utilizado para representar um número. Por exemplo, um nibble representa números não sinalizados de 0 a 24-1 = 15.
5.3- Números sinalizados
No sistema decimal, representamos um número negativo com o sinal "-". E como funciona no sistema binário?
No sistema binário, utilizamos o bit mais significativo (o bit mais à esquerda) para indicar o sinal. Dessa forma:
- Se o bit mais significativo for "0", o número é positivo.
- Se o bit mais significativo for "1", o número é negativo.
Exemplos (número de 8 bits):
01010101 - Positivo
11111110 - Negativo
Assim, um número "perde" sempre um bit para a sua representação. No caso de 8 bits, temos 7 bits para representar números positivos e 7 bits para representar números negativos.
Dessa forma, representamos:
- Positivos: de 0 a 127 (27-1).
- Negativos: de 1 a 128 (27).
E para 16 bits, temos:
- Positivos: de 0 a 32765 (215-1).
- Negativos: de 1 a 32768 (215).
Obs: para os números negativos, não existe o "-0". Por isso, ele começa do -1 e vai até -128 ou -32768.
Conforme visto, o valor de um número sinalizado é representado pelos outros bits restantes ao bit de sinal. Por exemplo:
01010101 - Positivo
11111110 - Negativo
O sinal está destacado em verde e o número em amarelo.
Para números positivos, o valor é obtido diretamente do número binário. No exemplo anterior:
1010101 = 85
Assim, o número sinalizado &B01010101 corresponde ao valor decimal +85.
Já o número negativo, devemos obter o complemento do número e depois somar mais um, pois o número negativo começa de -1 e não de 0.
O exemplo a seguir parte de um número binário sinalizado, de forma a obter o correspondente decimal sinalizado:
Número negativo:
11111110
Obtemos somente o número:
1 1111110
1111110
Complemento:
0000001
Mais um:
0000010
Valor em decimal: 2
Como é negativo, fica -2.
Para obter o binário sinalizado, a partir do decimal sinalizado, fazemos:
Valor decimal: -2
Valor binário (sem sinal):
0000010
Complemento:
1111101
Soma mais um:
1111110
Adiciona sinal:
11111110
Faixa de valores de números sinalizados de 8 bits:
Decimal | Binário
--------+---------
+127 | 01111111
+126 | 01111110
... | ...
3 | 00000011
2 | 00000010
1 | 00000001
0 | 00000000
-1 | 11111111
-2 | 11111110
-3 | 11111101
... | ...
-127 | 10000001
-128 | 10000000
No capítulo 6, veremos que há duas instruções em Assembly que fazem essas conversões para nós. A instrução CPL calcula o complemento de um número, enquanto que a instrução NEG calcula o valor negativo correspondente a um número positivo ou o valor positivo correspondente a um número negativo.
Por exemplo, para o CPL:
LD A,1
CPL
A operação realizada foi:
A = 00000001
CPL
A = 11111110
Já para NEG:
LD A,1
NEG
A operação realizada foi:
A = 00000001 (+1)
NEG
A = 11111111 (-1)
Mas vale também:
LD A,&HFF
NEG
A operação realizada foi:
A = 11111111 (-1)
NEG
A = 00000001 (+1)
