AI - Aprendizado Supervisionado

Inteligência Artificial
Aprendizado Supervisionado - Perceptron

Você está em: MarMSX >> Cursos >> AI Foi visto nos capítulos anteriores, como no jogo da velha, nos sistemas especialistas e na interpretação da linguagem humana, a necessidade de especialistas humanos tanto na área em questão, como em programação. Esses especialistas devem estabelecer todas as operações e introduzir o conhecimento necessário para que o programa seja capaz de reconhecer padrões e tomar decisões.
A proposta do aprendizado de máquina é possibilitar ao computador aprender através de exemplos fornecidos a ele, onde um conjunto de treinamento é fornecido com dados entradas que possuam saídas correspondentes (alvo ou gabarito). Enquanto que nos modelos tradicionais o programador é responsável por modelar o conhecimento, nos sistemas de aprendizado de máquina o processo de aprendizado é quem modela o conhecimento.
Uma comparação interessante [1] entre os sistemas tradicionais e o aprendizado de máquina é que no primeiro, criamos uma função para produzir respostas a partir de certas entradas. Já o segundo, o algoritmo utiliza o par entrada-saída para criar a função.
Espaço das características Texto adaptado de [2]

De modo a entender como o computador pode aprender e também modelar seu aprendizado, vamos utilizar o exemplo de um biólogo que deseja identificar a que mamífero pertence determinado crânio. Duas medidas utilizadas são o comprimento e largura máxima do crânio, que dão uma idéia grosseira do formato do crânio do animal.
A partir dos dados da altura e largura de crânios de lontras e minks, tentaremos identificar as duas espécies.
Para nós, humanos, analisar os dados numéricos e tentar concluir algo a partir dos números é uma tarefa difícil, principalmente se o conjunto de dados possuir milhares de elementos. Observe os valores das medidas dos crânios de lontras e minks e tente reconhecer as classes.

   Crânio
Largura Altura
3.0	7.0
3.6	9.0
3.8	6.5
5.6	4.0
5.8	3.0
4.1	7.5
4.4	8.5
4.6	6.0
4.0	2.0
4.2	3.0
4.4	4.0
4.6	2.0
4.8	3.0
5.0	4.0
5.2	2.0
5.4	3.0
6.0	4.0
3.3	8.0

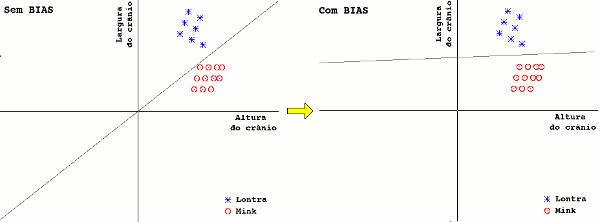
Entretanto, quando representamos os dados graficamente, fica evidente nossa maior capacidade de reconhecer padrões, pois somos especialistas nisto. Observe o gráfico a seguir. Fica fácil distinguir as classes lontra e mink.

Com um pouco de sorte, as medidas de cada espécie se agruparão em diferentes regiões do gráfico. No exemplo anterior, as medidas das lontras se encontram em uma região distinta da região onde aparecem os minks. Caso os dados estejam muito esparsos (não haja agrupamento) ou as duas classes se misturem na mesma região, não podemos utilizar essa características para discriminar as espécies. A solução é utilizar outras características.
Entretanto, se os grupos estiverem bem separados, de forma que conseguimos inserir uma linha reta separando as duas classes, podemos classificar um novo elemento simplesmente verificando de que lado da linha ele está no gráfico.
Traduzindo em termos matemáticos, o lado da reta em que o ponto cai é dado pelo sinal de

W1*X1 + W2*X2

Onde:

X1 e X2 - Atributos ou características dos elementos.
W1 e W2 - Definem a posição e orientação da reta.

Para podermos classificar novos objetos, é necessário primeiro ajustar a reta, ou seja, encontrar os valores de W1 e W2 que posicione a reta que divida da melhor maneira as duas classes. Então, como ajustar os valores de W1 e W2?
Primeiramente, atribuímos valores arbitrários a W1 e W2, pois nada sabemos a respeito deles. Uma reta qualquer, e provavelmente muito errada, é gerada para tentar separar as classes. Então, para ajustar os valores de W1 e W2, utilizaremos nosso conjunto de dados, pois são eles que contém a informação de que se a reta está ou não bem ajustada.
Nos aprendizados supervisionados, temos que indicar para cada elemento a que classe ele pertence, pois esse rótulo será utilizado para saber se a máquina está acertando ou errando na classificação durante o ajuste da reta.

   Crânio
Largura Altura	Classe
3.0	7.0	+1
3.6	9.0	+1
3.8	6.5	+1
5.6	4.0	-1
5.8	3.0	-1
4.1	7.5	+1
4.4	8.5	+1
4.6	6.0	+1
4.0	2.0	-1
4.2	3.0	-1
4.4	4.0	-1
4.6	2.0	-1
4.8	3.0	-1
5.0	4.0	-1
5.2	2.0	-1
5.4	3.0	-1
6.0	4.0	-1
3.3	8.0	+1

O aprendizado supervisionado é quando o computador necessita de que um "professor" lhe ensine a distinguir padrões nos dados. No exemplo acima, indicamos a que classe pertence cada elemento. Já o aprendizado não supervisionado é quando o computador é capaz de descobrir padrões nos dados por si só. No exemplo acima, o computador seria capaz de encontrar as duas classes a partir dos dados sem os rótulos. Veremos este tipo no próximo capítulo.

Para cada elemento do conjunto de dados testado, verificamos se a classificação foi correta ou não. Se sim, os valores de W1 e W2 estão corretos para aquele elemento. Entretanto, se a classificação estiver errada, será necessário ajustar os valores de W1 e W2.

Uma das maneiras de se ajustar a reta é movê-la a uma distância fixa na direção correta de um ponto classificado de forma errada.

Se o ponto for positivo (rótulo):
W1 = W1 + a*X1
W2 = W2 + a*X2

Se o ponto for negativo (rótulo):
W1 = W1 - a*X1
W2 = W2 - a*X2

Onde "a" é uma constante que controla a velocidade de aprendizado.

Cada iteração (loop) irá testar todos os dados, melhorar os valores de W1 e W2 e contar o número de classificações erradas. Quando o número de erros for igual a zero ou apresentar um número de erros aceitável, podemos dizer que a reta foi ajustada.
O processo de ajustar a reta chamamos de aprendizado e o conjunto utilizado para "ensinar" o computador é chamado de conjunto de treinamento.
O perceptron Os Engenheiros de Computação se basearam nos conceitos de bilogia para imitar o funcionamento do cérebro humano, com base nas características dos neurônios e nas ligações e troca de informações entre eles.
O perceptron modela um neurônio, no qual recebe informações através de seus dendritos e, através de uma função de ativação, envia um sinal.

Cada dendrito recebe um sinal de outro neurônio. Os cientistas perceberam que cada ligação entre os neurônios fica mais forte ou mais fraca de acordo com a importância dela no processo de aprendizagem de determinados padrões. Então, a cada entrada "E" associamos um peso "W", que indica o quão forte ou fraca é essa ligação.
No perceptron, adicionamos uma nova entrada chamada "bias", onde seu valor de entrada é sempre 1, mas também possui um peso associado a ele. O objetivo do bias é permitir o deslocamento da reta da origem.

Todas as entradas multiplicadas pelos respectivos pesos são somadas e processadas pelo neurônio. A função de ativação de um perceptron estabelece um limiar a soma dos valores de entradas, que quando atingido ou superado, envia um sinal. Dessa forma:

SUM = (E₁ * W₁ + E₂ * W₂ + ... + E_n * W_n + bias)

IF SUM > limiar THEN S=1 ELSE S=0

O processo de aprendizagem consiste em utilizar dados rotulados, chamados de conjunto de treinamento, para ajustar os pesos do neurônio. Nessa etapa, atribuímos pesos com valores aleatórios (de preferência valores baixos) e avaliamos todo o conjunto de treinamento. A cada classificação errada, corrigimos os pesos da seguinte forma:

W_n = W_n + η * (T - S) * E_n
bias = bias + η * (T - S)

Onde:

W_n - Peso.
η - Taxa de aprendizagem, varia de 0 a 1. Valores muito pequenos demoram a convergir e valores muito altos podem nunca convergir ou saltar o melhor ajustamento de pesos.
T - Rótulo do elemento "i" do conjunto de treinamento (saída esperada).
S - Saída obtida para o elemento "i" do conjunto de treinamento (saída obtida).
E_n - Entrada.

Assim como na seção anterior, a cada iteração - chamada de época, visitaremos todos os dados de treinamento e iremos obter uma taxa de erro. Podemos finalizar o treinamento quando a taxa de erro atingir um limiar aceitável ou determinar um número de épocas máximo.

O programa a seguir irá treinar o MSX para distinguir entre duas espécies de flores íris [3]: íris setosa e íris versicolor. Iremos utilizar os atributos comprimento e largura das pétalas, mais um rótulo dizendo a que classe aqueles dados pertencem: 0 para setosa, 1 para versicolor. Os rótulos são inseridos na linha 750.
As entradas do perceptron serão os dois atributos da flor íris: entrada 1 para o comprimento da pétala e a entrada 2 para a largura da pétala. A saída será 0 para a classe setosa e 1 para a classe versicolor.

Com o objetivo de avaliar o resultado do treinamento, separamos 70% dos dados de cada espécie para o treinamento e 30% para os testes. É importante não utilizar os dados de treinamento na realização dos testes de avaliação, pois isso poderia "mascarar" o sobreajuste, ou seja, o ajuste dos pesos funcionaria corretamente para o conjunto de dados utilizados no treinamento, mas teria desempenho ruim para novos conjuntos de dados.
A parte não utilizada no treinamento é como se fosse um novo conjunto de dados, pois não fez parte do treinamento, mas que possui um rótulo para avaliar a classificação.

No programa a seguir, não utilizamos os rótulos dos dados na hora de avaliar o conjunto de testes através do perceptron. Somente utilizamos os rótulos do conjunto de testes para ver se a classificação foi correta ou não.

5 ' Perceptron - MarMSX 2020
10 SCREEN 0:COLOR 15,0,0:WIDTH 40:KEY OFF
20 PRINT"Preparando dados ...":GOSUB 700
40 PRINT"Iniciando treinamento ..."
100 '
101 ' Treinamento
102 '
110 NE=5 : TA=0.05 : NT=35: TT=NT*2 : B=RND(-TIME)*.15
120 W1=RND(-TIME)*.15 : W2=RND(-TIME)*.15
120 FOR EP=1 TO NE
130 ET=0
140 FOR X=1 TO NT
150 E1=P(X,1):E2=P(X,2):T=P(X,3):GOSUB 500:GOSUB 600
160 E1=P(X+50,1):E2=P(X+50,2):T=P(X+50,3):GOSUB 500:GOSUB 600
170 NEXT X
180 PRINT"Epoca:";EP;" - Erro:";ET/TT
190 NEXT EP
200 '
201 ' Avalia conjunto de testes
202 '
210 ET=0:PRINT:PRINT"Avaliando conjunto de testes ..."
220 FOR X=36 TO 50
230 E1=P(X,1):E2=P(X,2):T=P(X,3):P=X:GOSUB 500:GOSUB 300
240 E1=P(X+50,1):E2=P(X+50,2):T=P(X+50,3):P=X+50:GOSUB 500:GOSUB 300
250 NEXT X
260 PRINT"Total de erros:";ET:PRINT
270 PRINT"Peso 1:";W1:PRINT"Peso 2:";W2:PRINT"Bias:";B
280 PRINT:PRINT"Tecle algo para ver graficamente ..."
290 A$=INPUT$(1) : GOTO 1000
300 PRINT"Elemento:";P;" - Alvo:";T;" - Avaliado:";S
310 IF S<>T THEN ET=ET+1
320 RETURN
500 '
501 ' Avalia entradas
502 '
510 IF (E1*W1 + E2*W2 + B) >= 0.5 THEN S=1 ELSE S=0
520 RETURN
600 '
601 ' Atualiza pesos
602 '
610 E = T-S
620 W1 = W1 + TA*E1*E
630 W2 = W2 + TA*E2*E
640 B = B + TA*E
650 ET=ET+E^2
660 RETURN
700 '
701 ' Define 100 pontos - IRIS setosa/versicolor
702 '
710 NP=100
720 DIM P(NP,3)
730 FOR I=1 TO NP
740 READ P(I,1),P(I,2)
750 IF I<51 THEN P(I,3)=0 ELSE P(I,3)=1
760 NEXT I
770 RETURN
800 DATA 1.4,0.2,1.4,0.2,1.3,0.2,1.5,0.2,1.4,0.2,1.7,0.4
810 DATA 1.4,0.3,1.5,0.2,1.4,0.2,1.5,0.1,1.5,0.2,1.6,0.2
820 DATA 1.4,0.1,1.1,0.1,1.2,0.2,1.5,0.4,1.3,0.4,1.4,0.3
830 DATA 1.7,0.3,1.5,0.3,1.7,0.2,1.5,0.4,1.0,0.2,1.7,0.5
840 DATA 1.9,0.2,1.6,0.2,1.6,0.4,1.5,0.2,1.4,0.2,1.6,0.2
850 DATA 1.6,0.2,1.5,0.4,1.5,0.1,1.4,0.2,1.5,0.2,1.2,0.2
860 DATA 1.3,0.2,1.4,0.1,1.3,0.2,1.5,0.2,1.3,0.3,1.3,0.3
870 DATA 1.3,0.2,1.6,0.6,1.9,0.4,1.4,0.3,1.6,0.2,1.4,0.2
880 DATA 1.5,0.2,1.4,0.2,4.7,1.4,4.5,1.5,4.9,1.5,4.0,1.3
890 DATA 4.6,1.5,4.5,1.3,4.7,1.6,3.3,1.0,4.6,1.3,3.9,1.4
900 DATA 3.5,1.0,4.2,1.5,4.0,1.0,4.7,1.4,3.6,1.3,4.4,1.4
910 DATA 4.5,1.5,4.1,1.0,4.5,1.5,3.9,1.1,4.8,1.8,4.0,1.3
920 DATA 4.9,1.5,4.7,1.2,4.3,1.3,4.4,1.4,4.8,1.4,5.0,1.7
930 DATA 4.5,1.5,3.5,1.0,3.8,1.1,3.7,1.0,3.9,1.2,5.1,1.6
940 DATA 4.5,1.5,4.5,1.6,4.7,1.5,4.4,1.3,4.1,1.3,4.0,1.3
950 DATA 4.4,1.2,4.6,1.4,4.0,1.2,3.3,1.0,4.2,1.3,4.2,1.2
960 DATA 4.2,1.3,4.3,1.3,3.0,1.1,4.1,1.3
1000 '
1001 ' Plota resultado
1002 '
1010 SCREEN 2:FX=255/6:FY=191/2
1020 FOR I=1 TO 100
1030 X=P(I,1)*FX : Y=191-P(I,2)*FY
1035 E1=P(I,1):E2=P(I,2):GOSUB 500
1040 IF S=0 THEN C=2 ELSE C=5
1050 PSET(X,Y),C
1060 NEXT I
1070 GOTO 1070

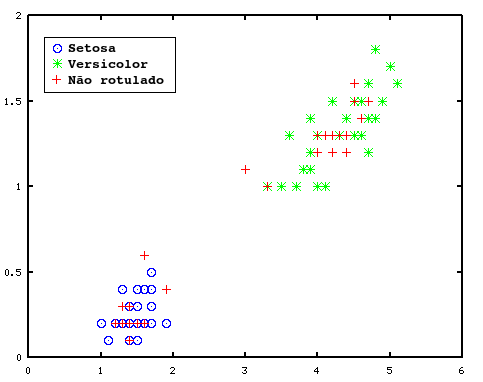
O treinamento converge em apenas duas épocas. Todo o conjunto de testes é avaliado e nenhum erro é encontrado. Então, os valores dos pesos e do bias são apresentados e ao final, um gráfico é gerado com a classificação de todo o conjunto de dados: verde para a classe setosa e azul para a versicolor.

Entretanto, nem tudo são flores! Se utilizarmos as espécies versicolor e virgínica do mesmo conjunto íris, onde há pequena interseção dessas duas espécies quando visualizadas no gráfico, iremos notar que algumas espécies serão sempre classificadas incorretamente, além de demorar muito mais para convergir.

Altere as seguintes linhas do programa anterior:

110 NE=50 : TA=0.05 : NT=35: TT=NT*2 : B=RND(-TIME)*.15
...
780 DATA 4.7,1.4,4.5,1.5,4.9,1.5,4.0,1.3
790 DATA 4.6,1.5,4.5,1.3,4.7,1.6,3.3,1.0,4.6,1.3,3.9,1.4
800 DATA 3.5,1.0,4.2,1.5,4.0,1.0,4.7,1.4,3.6,1.3,4.4,1.4
810 DATA 4.5,1.5,4.1,1.0,4.5,1.5,3.9,1.1,4.8,1.8,4.0,1.3
820 DATA 4.9,1.5,4.7,1.2,4.3,1.3,4.4,1.4,4.8,1.4,5.0,1.7
830 DATA 4.5,1.5,3.5,1.0,3.8,1.1,3.7,1.0,3.9,1.2,5.1,1.6
840 DATA 4.5,1.5,4.5,1.6,4.7,1.5,4.4,1.3,4.1,1.3,4.0,1.3
850 DATA 4.4,1.2,4.6,1.4,4.0,1.2,3.3,1.0,4.2,1.3,4.2,1.2
860 DATA 4.2,1.3,4.3,1.3,3.0,1.1,4.1,1.3,6.0,2.5,5.1,1.9
870 DATA 5.9,2.1,5.6,1.8,5.8,2.2,6.6,2.1,4.5,1.7,6.3,1.8
880 DATA 5.8,1.8,6.1,2.5,5.1,2.0,5.3,1.9,5.5,2.1,5.0,2.0
890 DATA 5.1,2.4,5.3,2.3,5.5,1.8,6.7,2.2,6.9,2.3,5.0,1.5
900 DATA 5.7,2.3,4.9,2.0,6.7,2.0,4.9,1.8,5.7,2.1,6.0,1.8
910 DATA 4.8,1.8,4.9,1.8,5.6,2.1,5.8,1.6,6.1,1.9,6.4,2.0
920 DATA 5.6,2.2,5.1,1.5,5.6,1.4,6.1,2.3,5.6,2.4,5.5,1.8
930 DATA 4.8,1.8,5.4,2.1,5.6,2.4,5.1,2.3,5.1,1.9,5.9,2.3
940 DATA 5.7,2.5,5.2,2.3,5.0,1.9,5.2,2.0,5.4,2.3,5.1,1.8
...
1010 SCREEN 2:FX=255/7:FY=191/3

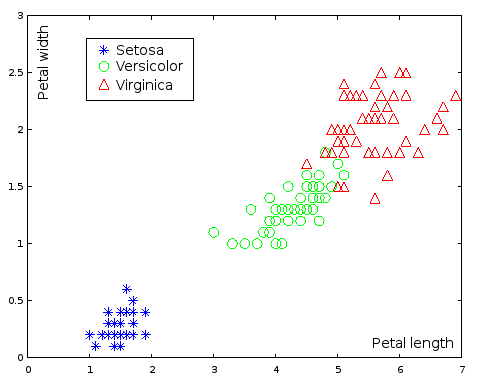
Saída gráfica:

Os pontos verdes agora representam a classe versicolor, enquanto que os azuis a classe virgínica.

O perceptron tem a limitação de apenas conseguir distinguir classes linearmente separáveis, ou seja, onde somente podemos discriminar classes através de uma reta.
Para problemas não lineares, devemos utilizar mais perceptrons (ou neurônios) e formar uma rede neural mais complexa. A essa estrutura chamamos de Multilayer Perceptron.
As redes neurais são capazes de modelar diversos tipos de problemas de um alto grau de complexidade. Atualmente, são utilizadas em diversas aplicações como, por exemplo, reconhecimento de voz, imagens, sistemas de previsão e classificação de dados.

Referências

1. Inteligência Artificial para Leigos, J. P. Mueller e L. Massaron. Ed. Alta Books, 2019.
2. Inteligência Artificial em Basic, Mike James. Ed. Campus, 1985.
3. Iris, Repositório de dados da UCI. Em http://archive.ics.uci.edu/ml/index.php
4. Neural Java, Cleuton Sampaio. Editora Ciência Moderna, 2020.

<< Anterior

Próxima >>